1.1 Thermal Equilibrium¶
In this section, we talk a little bit about temperature and thermometers, and we start to define some useful terms. We’ll also think about what quantities are exchanged when two objects are brought into contact with each other, and to what equilibrium these changes tend towards.
Finally, we’ll describe temperature scales without going into too much detail of how they work.
With a decent understanding of temperature, we can begin to reason about thermal physics.
Temperature¶
Naive definition:
Temperature is what you measure with a thermometer.
“Naive” because it shows a great lack of understanding of what temperature really is and what thermometers actually are. And it is entirely dependent on a physical device – the thermometer.
Regardless, we need to start somewhere.
This is actually a good “Operational Definition”:
Operational Definition: A definition that tells you HOW to measure the quantity.
Why do thermometers work?
In a mercury thermometer, temperature changes the mercury such that it either expands or contracts. You are really seeing how big the mercury is, and inferring from that the temperature. You are not measuring the temperature directly.
What happens when I have two thermometers? Will they agree? What if they don’t agree? Is one broken or is this a pointless exercise in futility? What if they are made of different materials?
Let’s try another definition:
Temperature is the thing that is the same for two objects, after they’ve been in contact long enough.
This is a “theoretical definition”. It describes temperature not as an observable quantity, but as an invented, magical substance that obeys seemingly arbitrary laws.
Our ancestors had plenty of ideas of theoretical quantities and substances! Ever hear of “Caloric” or “Phlogiston”? The classical element of “fire” or Aristotle’s property of “hot”?
We need specifics!
What is “contact”?
How long is “long enough”?
Is there some other thing that becomes the same?
More definitions:
Thermal equilibrium is the state of the two objects after they have been in contact long enough.
Relaxation time is how long it takes to reach thermal equilibrium.
Footnote: Some people say this is when the temperature difference has reduced
by a factor of 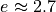 . In Schroeder, all he needs is a
qualitative definition – something that we can talk about even if we can’t
assign numbers to it.
. In Schroeder, all he needs is a
qualitative definition – something that we can talk about even if we can’t
assign numbers to it.
Note that when you use a thermometer it takes some time to get a reading. If I were to read it while the number is changing because it is coming into thermal equilibrium, I would get the wrong answer. So I need to wait until the number stops changing!
What does “contact” mean? It means we allow the two objects to exchange energy spontaneously – on their own. We call this energy so exchanged “heat”. (“Heat” means a lot of things, but I will be careful only to use it correctly.)
We can put the two objects in direct contact with each other. IE, put the cup of hot chocolate on the counter, or let it interact with the air.
We can show there is an energy exchange even when there is a vacuum, through radiation.
We can try to prevent the energy from spontaneously exchanging, by putting some kind of thermal insulation between them, but all we are really doing is greatly increasing the relaxation time. Given enough time, they will still thermally exchange energy.
We already have an intuitive grasp on what the relaxation time should be for most day-to-day objects. He uses the example of a cup of hot chocolate. When you add cream, the cream almost instantly takes on the temperature of the hot chocolate (and cools it down.) But you can leave out the cup of hot chocolate for several minutes before it grows cold on the counter.
Consider the cream in the hot chocolate. We start off with a clear boundary between the cream and the hot chocolate, but in the end, they mix together and we now have a mixture of cream and hot chocolate, where we can no longer distinguish the cream from the hot chocolate. This certainly means that the cream and the hot chocolate have taken on the same temperature, but it also introduces a new sort of equilibrium – diffusive equilibrium. “Diffuse” means to “spread out”. Particles of cream have thoroughly mixed with the particles of hot chocolate to the point where they are indistinguishable.
There is another kind of equilibrium – mechanical equilibrium – where two objects obtain the same pressure as each other by altering their mutual volumes. Say, for instance, you had a balloon. As I put air into the balloon, it grows bigger, but the atmosphere is also pushing on it. Why doesn’t the balloon grow to fill the room, or shrink to its original size?
We can draw a table:

Now we know that when we bring two objects into contact, that there are at least three quantities exhanged to obtain three types of equilibrium.
Let’s talk about thermal equilibrium – the temperature. When one object is hotter than the other, heat flows from it to the colder object.
Now we can better define temperature:
Temperature is the measure of the tendency of an object to spontaneously give up energy to its surroundings. When two objects are in thermal contact, the one that tends to spontaneously lose energy is at the higher temperature.
Now we can not only tell when two objects have the same temperature, but we can arrange objects of various temperatures in order, and thus assign a quantity to the temperature!
(Chapter 3 covers temperature in much greater detail.)
Measuring Temperature¶
How do we measure temperature?
Most thermometers rely on thermal expansion, the tendency of objects to increase in volume or size when they get hotter (provided the pressure remains the same!)
IE, in a mercury thermometer, we can take a pot of boiling water at 1 atmosphere of pressure and stick the thermometer in there, wait until it stops moving, and them mark that “100”. Then we can stick the same thermometer into an ice bath, wait for equilibrium, and mark it as “0”. Then we carefully measure the distance between the two and make even marks, and we have our temperature scale! This is the definition of the Celsius scale, in degree centigrade.
What if we tried using different materials instead of mercury? Would they expand at the same rate throughout the range of temperatures? If my mercury thermometer measured 20 degrees centigrade, would the other thermometers measure the same?
What if we used different methods of measuring temperature. Let’s say a strip of metal that we carefully measure its expansion. Or we measure the resistance through a wire. Two metals sandwiched together, with different rates of expansion. Or we measure the voltage across the barrier of two metals. Or the pressure of a fixed quantity of gas.
In the book, he has a picture of potter’s cones. These are designed to melt at different temperatures. This can be useful as well.
Different thermometers work in different temperature ranges. The gas can get so cold it can condense into a liquid. Mercury can change phase into a solid (or a gas!) Alcohol boils at a relatively low temperature. Etc, etc, etc…
Ideally, we’d like to come up with a temperature scale that does not depend on the material. Surely, the universe has something to say about an absolute temperature scale! If such a thing existed, we can tune all of our thermometers to it.
Let’s play with the gas thermometer. If we were to use different gasses (or different quantities or volumes), we’d see that they form a graph giving us their particular pressures at particular temperatures. These lines point to a particular spot – where hte pressure would be zero! Now, obviously, if we tried to cool these gasses down to this temperature, at some point they would condense into a liquid and then into a solid, spoiling the measurements. But isn’t it interesting how they all point to the same point? On the Celsius scale, this is -273 degrees centigrade or so. If we adjusted the Celsius scale so that 0 was this temperature, then we would have the kelvin scale. Each degree is still the same distance apart as it is for Celsius, but room temperature is now around 300 degrees kelvin.
This temperature has a special name: absolute zero.
Using kelvin has many benefits, namely the fact that we don’t have to add 273 everywhere.
Problem Solving Tips¶
These problems range from the ridiculously easy to the easy. No advanced math beyond basic geometry and algebra are needed.
1.1: This should be easy. It’s a simple linear equation.
1.2: Should be easy.
1.3: Human body temperature is 98 degrees Fahrenheit or 37 degrees centigrade. Water boils at 100 degrees centigrade or 212 degrees Fahrenheit. The coldest day you can remember depends on where you’ve lived. Where I live now, it seldom drops below zero on the Fahrenheit scale. I have heard of relatives living in places where it gets all the way down to 50 below Fahrenheit. If you live in Antarctica, you might see temperatures well below 100 degrees Fahrenheit.
1.4: Temperature, in a sense, is a measure of the potential to heat other things up. What do you think “twice as hot” should mean?
1.5: Nowadays we have instant medical temperature devices. I don’t trust them. I rely on the electronic stick-it-in-your-mouth thermometers.
1.6: If you’re having a hard time thinking of things, imagine it is a cold day outside. Which would feel colder: a piece of metal or a piece of wood? Aren’t they supposed to be in thermal equilibrium with the weather outside? Or on a hot sunny day, would you rather walk barefoot on grass, concrete, sand, a wooden deck, or metal sheets? Assuming that they aren’t in direct sunlight, shouldn’t these all be the same temperature?
1.7: I suggest looking up the dimensions of a mercury thermometer online, (Hint: they are pretty standard.) It may be difficult to get your hands on one because mercury is known to be toxic and glass is known to break. If you wish, create your own mercury thermometer in your imagination based on the pictures you see online.
For (b), consider the fact that ice floats. Did the water expand or contract before it changed to ice? What would happen if water continued to contract as it froze – would ice sink or float? A good experiment to try here is to actually freeze liquids that do not expand as they freeze and observe how their crystals form. Observe how ice forms in a cup of water in the freezer by examining it as it freezes from time to time.
1.8: (a) Look up the highs and lows of the region of the world you live in. (b) Think of how the metal coil would change its shape if one of the metals shrunk faster or grew faster than the others. Consider that they are not at the same radius of curvature – one is on the outside and thus travels a longer path around the curve! (c) If a solid expands in all directions by this constant amount, how will its volume change?
If you need more homework help, join me on Discord or ask in the comments below. Please be sure to add some sort of spoiler message so people trying to solve the problem on their own won’t have it spoiled.
If you are legitimately having a difficult time with this, it may be because you’re rusty on your math skills. Find me on Discord, let me give you a simple test to see where you’re at and I can recommend a course of action.

